OPERASI PADA FUNGSI

OPERASI PADA FUNGSI

JIka ada dua fungsi:  f(x)  dan  g(x) ,  maka berlaku:

1.  (f + g)(x)  =  f(x) + g(x)

2.  (f – g)(x)  =  f(x) – g(x)

3.  (f x g)(x)  =  f(x) . g(x)

4. (f/g)(x) = f(x) / g(x)

 5.   fⁿ(x)  =  [ f(x) ]ⁿ

Contoh :

Jika  f(x) = 2x – 3  dan  g(x) = 4 – x  maka tentukan:

a. (f+g)(x)        b. (f – g)(x)      c. (f x g)(x)      d.(f/g)(5)         e. f²(-1)

Jawab:

a.  (f + g)(x)  =  2x – 3   +   4 – x  =   x + 1

b.  (f – g)(x)  =  2x – 3  –  (4 – x)  =   3x – 7

c.  (f x g)(x)  =  (2x – 3) x (4 – x)  = –2x² + 11x – 12

d.gambar

e.  (f)²(x)  =  (2x – 3)² =  4x² – 12x + 9    ®  (f)²(-1) = 25

Fungsi Komposisi

(g o f)(x) = g(f(x)) , artinya:  f(x) masuk ke g(x)

Contoh:

Jika  f(x) = 2x – 5  dan  g(x) = 3x + 1

tentukan:    a.  (f o g)(x)          b.  (g o f)(x)          c.  (f o g)(4)

Jawab:

a.  (f o g)(x)  =  f(g(x))  =  2(3x + 1) – 5  =  6x – 3

b.  (g o f)(x)  =  g(f(x))  =  3(2x – 5) + 1  =  6x – 14

c.  (f o g)(4)  =  6 . 4 – 3  =  21

nah, buat latihan silahkan cobakan soal berikut …

A. Tentukan  (f o g)(x)  & (g o f)(1)  jika:

            1.  f(x) = x² – 4  ,    g(x) = x + 3

            2.  f(x) = x² – x – 6  ,    g(x) = x² + 2

B. Tentukan  f(x – 2)  jika:

            1.  f(x) = 3x + 7

            2.  f(x) = x² + x – 12

C. Tentukan f(x)  jika:

            1.  f(x + 3) = 6 – 5x

            2.  f(2x – 7) = 4x – 3

            3.  f(2 – x) = x² – 10

Menentukan  f(x)  atau  g(x)  jika diketahui komposisinya

Contoh:

1.  Jika  (f o g)(x) = 6x – 5  dan  f(x) = 2x + 1  maka  g(x) = ?

Jawab:

Cara 1 :  (f o g)(x)  dan  f(x)  linear ®  misal  g(x) = ax + b

(f o g)(x) = f(g(x))

6x – 5  =  2 (ax + b) + 1  =  2ax + 2b + 1

†  g masuk ke f => 2a = 6  ®  a = 3 , 2b + 1 = –5 ®  b = –3

didapat  g(x) = 3x – 3 , silakan cek  (f o g)(x) = . . . . ?

Cara 2 :  yg diketahui  (f o g)(x)  dan  f(x)

(f o g)(x) = f(g(x))

6x – 5  =  2 g + 1   , 2g = 6x – 6 , g(x) = 3x – 3

2.  Jika  (f o g)(x) = 6x – 5  dan   g(x) = 2x + 1  maka  f(x) = ?

Jawab:

Cara 1 :   (f o g)(x)  &  g(x)  linear  ®  misal  f(x) = ax + b

(f o g)(x) = f(g(x)) maka  6x – 5  =  a(2x + 1) + b  =  2ax + a + b

2a = 6  ®  a = 3          , a + b = –5   ®  b = –8

didapat  f(x) = 3x – 8 , cek  (f o g)(x) = . . . . ?

Cara 2 :   yg diketahui (f o g)(x)  dan  g(x)

misal g(x) = 2x + 1 = a maka x = (a-1)/2

f(a) = 6(a-1)/2 -5

f(x) = 3x – 8

buat latihan cobain nih !!!

1.  Tentukan  f(x)  jika:

            a.  (f o g)(x) = 4x + 7 ,  g(x) = 2x

            b.  (f o g)(x) = x² + 3x – 6 , g(x) = x + 1

            c.  (f o g)(x) = x² + 3x – 18 ; g(x) = 2 / (x+1)

            d.  (f o g)(x – 2) = x² + x – 12 ,  g(x) = x + 3

2.  Tentukan  f(x)  jika:

a.  (g o f)(x) = 4x + 7 , g(x) = 2x

b.  (g o f)(x) = x² + 3x – 6 ,  g(x) = x + 1

c.  (g o f)(x) = x² + 3x – 18 ; g(x) = 2 / (x+1)

d.  (g o f)(x – 2) = x² + x – 12 ,  g(x) = x + 3

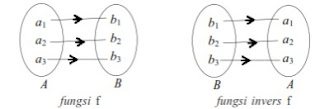
FUNGSI INVERS

Jika fungsi f = A→B dinyatakan dengan pasangan terurut f = {(a, b) | a ∈ A dan b ∈ B}

maka invers fungsi f adalah f-1= b→A ditentukan oleh f-1 = {(b, a) | b ∈ B, dan a ∈ A}.

Untuk menentukan fungsi invers dari suatu fungsi dapat dilakukan dengan cara berikut ini.

a. Buatlah permisalan f(x) = y pada persamaan.

b. Persamaan tersebut disesuaikan dengan f(x) = y, sehingga ditemukan fungsi dalam

            y dan nyatakanlah x = f(y).

c. Gantilah y dengan x, sehingga f(y) = f(x).